In this lecture, we generalized our setting to weighted graphs  where
where  is a positive weight function on edges. We also looked at the basic spectral theory of the normalized Laplacian, defined by
is a positive weight function on edges. We also looked at the basic spectral theory of the normalized Laplacian, defined by
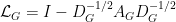 ,
,
which operates on functions 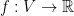 via
via
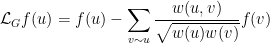 .
.
In particular, we associated with 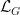 the normalized Rayleigh quotient,
the normalized Rayleigh quotient,
 ,
,
and we showed that we can express the second-smallest eigenvalue as
 .
.
We defined the expansion of a subset  by
by
 ,
,
where 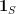 is the characteristic function for
is the characteristic function for 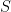 .
.
Finally, we defined the expansion of a graph by

We then stated and (almost) proved the following discrete Cheeger inequality.
Theorem 1. For any weighted graph  , we have
, we have
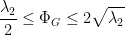 ,
,
where 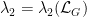 .
.
Exercises (optional)
- Prove that for the normalized Laplacian, just as for the combinatorial Laplacian, the number of connected components in a graph G is precisely the multiplicity of the smallest eigenvalue.
- We saw the the right-hand inequality in Theorem 1 is asymptotically tight. Prove that the left-hand side is asymptotically tight for the complete graph on n nodes.
and the mixing time of random walks
